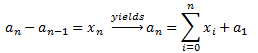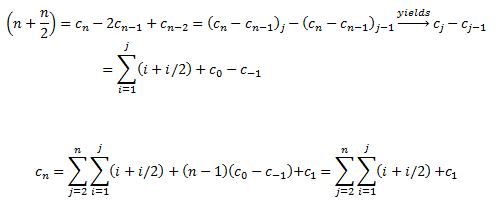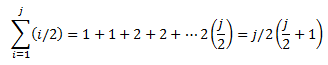Triangles Enumeration & Counting: Solution
 Francesco Abbruzzese
Francesco Abbruzzese
CTO Mvc Controls Toolkit
Enumeration
Enumeration problems are usually solved by looping on other objects that we are already able to enumerate , and then performing some processing on each of these objects in order to find some of the target objects. While performing this operation we must take care of avoiding duplications, and of ensuring completness.
In our case we may loop on all vertices looking for all triangles containing that vertex. However, this way we would have duplications since each triangle has three vertices, so it would be repeated three times. Duplications may be avoided by looking only for the triangles where the current vertex has a specific role, that is, either left vertex, or right vertex, or the other vertex (the one we called vc in the problem statement). All three choices produce all triangles without duplications.
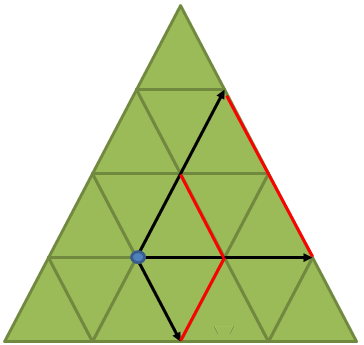
All triangles where a given vertex v plays the role of left vertex may be found by stepping on the three half lines that are on the right of the vertex:
More specifically, we step simultaneously on the up-right, and right half line to find all up tiangles, and simultaneously on the down-right and right half lines to find all upside down triangles. In each step we join the newly reached vertices to the current vertex to output a new triangle, till we reach a big triangle boundary on any of the two involved half lines.
If we choose to work with right vertices, the algorithm is completely symmetric.
All triangles where a given vertex plays the role of vc vertex, instead, are found by stepping along the up-left, and up-right half lines to find the up triangles, and by stepping along the down-lef and down-right half lines to find all down triangles, as shown in the image below:
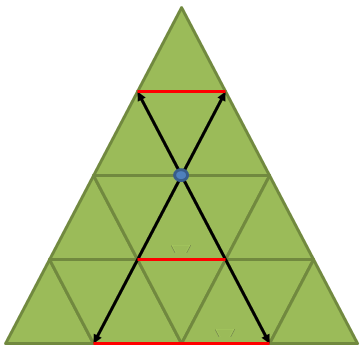
Thus, we have two main classes of algorithms, one based on left vertices (or summetrically right vertices) and one based on vc vertices.
In turn each of the above classes may be implemented in two ways, thus yielding a total of 4 conceptually different algorithms.
We may use the six vertex pointers in the problem statement (L, R UL, UR, DL, DR) to step along the half lines till a null pointer is reached or we may use mathematical computations to step along the half-lines.
In the last case we don't need at all a data structure containing all vertices, since the coordinates of all vertices found during the computation may be found dynamically with some simple math. However, the termination conditions of both the loops that enumerate all vertices, and the ones that step along the half lines are more difficult to compute. They may be found either by imposing inequalities on the coordinates, or by computing the number of steps with some linear math. Typically, when this solution is adopted, all equilateral triangles are transformed into 90-45-45 triangles. This way we move only along straight lines that are parallel to the x-y axes and the whole algorithm may be implemented with integer math, thus avoiding rounding errors due to the use of floating numbers.
The second solution is more difficult, but it is more useful if one has no precomputed data structure containing all vertices. Its main drawback is that vertices are not tokenized. This means that each triangle has a different copy of the same vertex instead of a pointer at an unique data structure representing the vertex. In theory tokenization might be achived during the algorithm execution, with the help of hash tables. However, this would have an unacceptable impact on the algorithm performance.
My choice was the vc vertex algorithm with the vertex pointers:
The full code is available here.
Counting
Counting reduces to the computation of a third degree polynomial:
The above formula may obtained by first writing a recursion relation, and then by solving it with standard math techniques. Calculations are not immediate, but the recursion formula is quite easy to obtain. More specifically, I found two ways to write a recursion relation:
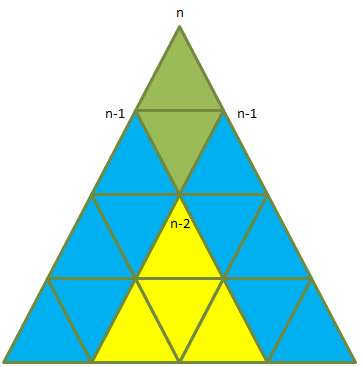
The more "standard way", is obtaining an n-triangle by adding a new row to an n-1 triangle, and counting how many triangles are cotributed by the addition of the new row:
However, the new triangles contributed are not so immediate to count. There is a simpler way to obtain a recursion relation:
An n-triangle may be obtained by superimposing two (n-1)-triangles along the common (n-2)-triangle, and then by adding a top vertex.
In this case the count for n may be obtained by summing the triangles contained inside the two (n-1) triangles (that is by taking twice the count for n-1, subracting once the the triangles contained in the common (n-2)-triangle that otherwise would be counted twice, and adding all other triangles that are not contained in either of the two (n-2) triangles.
It is easy to understand that only triangles that have both their left and right vertices on the two sides of the n-triangle are not completely contained in the (n-2)-triangles.
This means that the newly contributed up triangles are just:
That sum to n.
While the newly contributed down triangles are:
They sums to n/2, where / denotes the integer division, since only even rows may contain the vc vertex of these triangles.
Summing up the recursion equation is:
Now since:
we have:
Since for n=0, -1 the count is 0.
Now the first term is 1, while it is well known that the double sum on i yields (n+2)(n+1)n/(3*2). The i/2 term is a little bit more difficult to double sum because of the integer division. The basic trick to process it is:
When j is odd. When j is even the last term appears only once so we have j/2(j/2+1) - j/2.
The above result must be summed again from 1 to n. The computation may be done first considering the case n odd and then the case n even. Again for n odd the term j/2(j/2+1) is repeated twice, while for n even the last term appears only once. The j/2 term, instead, appears only in the even terms of the sum....The final result obtained after adding also the previous (n+2)(n+1)n/(3*2) term and c1=1 is: (n(n+2)(2n+1))/8 where the last division is an integer division.